AMBA Bus Architecture & Protocol Understanding - Part#3

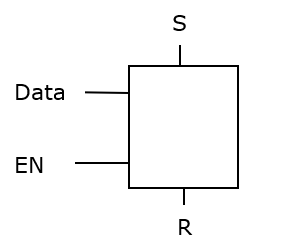
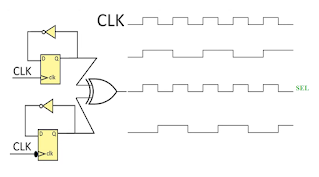
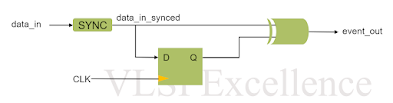
There are 2 basic reasons why AXI may be faster: 1) Simplex Vs Duplex Transfers AXI has completely independent channels for read/write, which enables full duplex mode of data transportation. That is to say read and writes can take place simultaneously, giving 2x boost over AHB in any circumstances....

Read More

AMBA Bus Architecture & Protocol Understanding - Part#1

Following diagram illustrates AMBA evolution of protocols along with the SOC design trends in industry.AMBA 1 specification (First version) defines two buses/interfaces- 1) Advanced System Bus (ASB) 2) Advanced Peripheral Bus (APB) AMBA 2 specification defines three buses/interfaces: 1) Advanced High-performance...

Read More

Power Aware Clock Domain Crossing

Chief Aspects of Power Management : · Power Shut-off · Isolation · Retention · Corruption · Multiple Voltages · Level shifters Note: Leakage Power Reduction is Key in Low-Power Design Power Network Instrumentation - · Presence of power network may impact CDC...

Read More

Design a Circuit for Retention SR Flip-Flop/Latch

SR Retention Flip-Flop/Latch : - Lets have a look at a normal SR Flip Flop and Latch as below - Figure#1 : SR Flip-Flop Figure#2 : SR Latch...

Read More

Unified Power Format (UPF) Design - key Points

1) Do we need any isolation strategy between ON - to - OFF (Standby) Block ? - Generally the isolation is required between OFF - to ON Block but in some cases it is recommended to use isolation between ON - to -OFF domain as well. - Normally the isolation strategy between OFF - to - ON is called as Parking - This kind of strategy is required for some special kind of signals which have...

Read More

Fundamentals of LINT

Lint : - A Static analysis of code (e.g HDL) based on a series of rules and guidelines that reflect good coding practices, common errors that tend to lead to buggy code or problems - Lint tools are used to check potential mismatches between simulation and synthesis in VLSI Design - Lint incorporates syntactical compliance checks against various coding best practice standards such...

Read More

Fundamentals of Isolation Cells in Low Power VLSI Design

In Multi Voltage VLSI Design, isolation cells play an important role in the modern VLSI world.Requirement : Lets have a look at the below diagram - - Lets assume VDDA voltage domain is always ON and VDDB voltage domain can go ON or OFF based on the certain design requirements ( To minimize the...

Read More

Digital Circuit Design - Problem#5

Problem: Design a digital circuit which can generate a pulse which is high for 16 clock cycles and then goes low (Active High Reset Signal)as shown in the below waveform Solution : - Lets have a look at previous problem where we discussed on how can we generate an active low reset...

Read More

Digital Circuit Design - Problem#4

Problem : Design a digital logic circuit to generate a reset pulse which is low for 16 clock cycles (Active Low Reset Generation) as shown in below waveform. Solution : - Here we need a output signal of the circuit which is low for 16 cycles and then becomes high - Can 16 flop in a cascade manner do...

Read More

Digital Circuit Design - Problem#3

Problem : Design a digital logic circuit to generate a stick bit as shown in the below waveform. The circuit takes an input as I/P and runs at a clock speed of CLK Solution : - Once the input is high the output should always remain high irrespective of whether the I/P signal is toggling at later point...

Read More

Digital Circuit Design - Problem#2

Problem : Design a black box circuit shown below whose input clock and output relationship is shown in below waveform. Solution : - Lets have a look at below circuit diagram - - Now lets see how the waveform looks like for this circuit - ...

Read More

Digital Circuit Design - Problem#1

Problem : Design a digital circuit as depicted in below block diagram which takes DIN as an input and runs at a clock speed of CLK and generates an output DATA as shown in the waveform below.Solution : - Since the circuit sample the data at both positive and negative edge of the clock, we need both...

Read More

Verilog HDL Examples - Design of an Event Detector (Circuit Design)

Problem : Design a circuit which detects and event (for one clock cycle) whenever there is a change (Either rising edge or falling edge)in the input signalSolution : 1) The input signal is asynchronous to the Event Detector logic domain -Note: The data_in must come out of a register from the source...

Read More

Tic-Tac-Toe Game Design Using Python

And here comes some fun in the time when we all are locked inside our homes because of this COVID-19 pandemic ( 05/25/2020) . I am going to guide you on how you can build your own Tic_Tac_Toe Game using Python scripts in just few minutes and can enjoy playing with your loved once.How to play Tic_Tac_Toe...

Read More

BlackJack Game Design Using Python

CASINO !!! Yes , You imagined Rightly. Let's see how in couple of minutes you can develop your own Black Jack Game using Python Scripting.Blackjack : Blackjack, formerly also Black Jack and Vingt-Un, is the American member of a global family of banking games known as "Twenty - One", whose relatives...

Read More